Reverse engineering curves – The Sagitta

Here’s something fun and useful. I love when I get to get all math-y…

A long time ago (2006), I put a blurb up on my wiki. It was a re-post from long ago that I had posted onto a skateboarding message board, probably back in 1998 or so. My web site, wiki, and now blog grew from having online discussions that were often full of misinformation repeated by lazy ‘scholars’… Let’s just say that most people online are literal retards… Controlling my content gave me the ability to control the concepts and define the debate. Always a powerful tool.

Back to the point. What I had posted is a graphic that shows a skateboarder how to measure the transitions that they may encounter at a skatepark or on a ramp. Often times, as a skater or any other rider of transition, you will ride something you really like or want to reproduce in another setting. Sadly, the skatepark world is quite neanderthal and not very mature in complex problem solving. Even in the real world, precision comparitors aren’t readily available or understood by many, but most folk do have access to yard sticks and tape measures. Really, just a tape measure is needed if you do the math in general form and make sure to measure the straight edge. This technique is scalable, though, so you could use blocks and pins for small stuff, or laser range finding for really big stuff.

Obviously, I put the math into specific form for when using a yard stick as the straight edge and inches for the displacement. The more general form is:

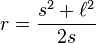$r={\frac {s^{2}+\ell ^{2}}{2s}}$ , where ‘s’ is the distance from the straight edge to the curve and ‘l’ is half the length of that edge.

This is all using a trigonometric descriptor known as the sagitta. Read up on it. Chords are rad!

This simple understanding is a great tool for a challenging reverse engineering problem in measuring curved structures and surfaces. Anybody who makes anything has to do this at some point. It’s important and it’s easy when you know how.

Some other cool things to do with this:

Mechanical measuring of the focal length of a lens or mirror in photography or astronomy. Focal_Length (F) = Mirror_Radius² / ( 4 × Sagitta )
Finding the bend radius for a tube on a bicycle or motorcycle
Arriving at the curve of the concave or rocker on a skateboard or surfboard.

Special tools do exist that can be quite precise. See the Precision Tool Tech unit.

Here, I’m using a depth micrometer in a fairly crude way (flat tip vs dome or point) to measure the sagitta of the chord of this radius. A handy trick.

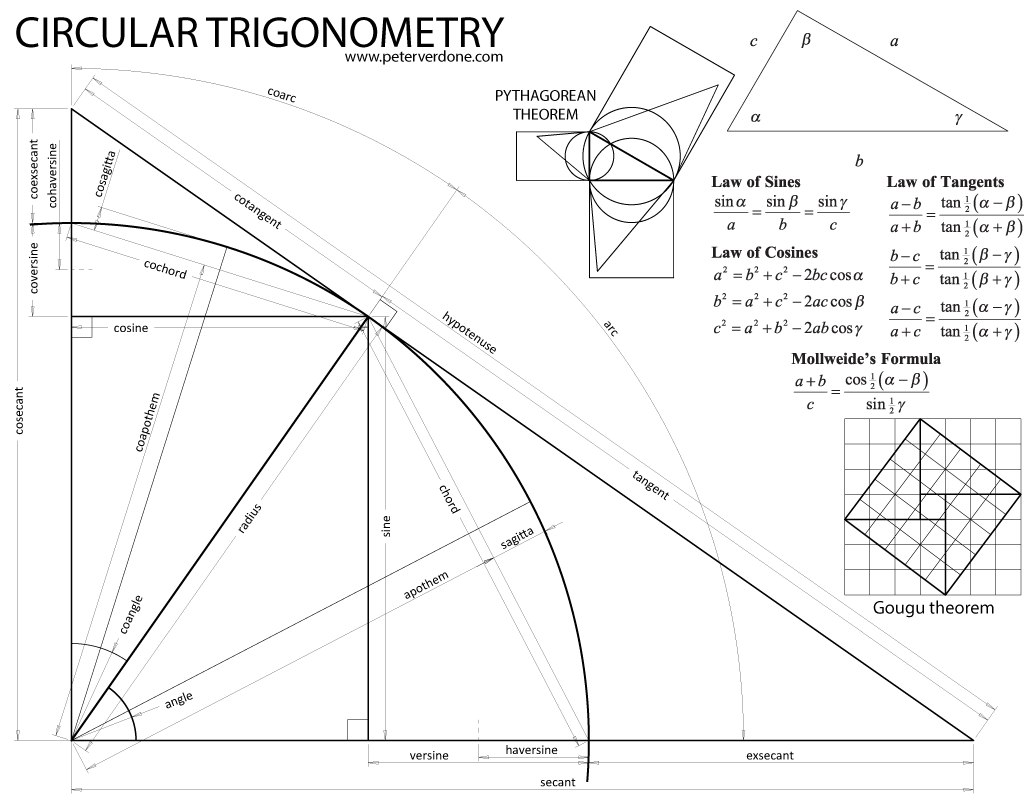
This post stemmed from a discussion that ensued on Facebook after I threw up an old post I did on trigonometry. I was reminded me of this cool thing.

Here’s that wonderful trig image: