POST: 2020/02/15 – An attempt has been made to refine the content you see here in a newer post. This should help a bit as it is clearer and more straightforward.
Last year, PinkBike published an article describing Lee McCormack’s concept of fitting bikes using his Rider Area Distance (LLB-RAD) method of bike fitting. McCormack describes this further on his own website. Pretty much anything PinkBike says about bike geometry or setup is wrong so I took this with an immediate grain of salt. Please, never listen to PinkBike, they have absolutely no idea what they are talking about!
The LLB-RAD dimension is the bottom bracket to the hand grip. Simple. Then he gets fancy.
“If you’re male, multiply your height in centimeters by 4.47
If you’re female, multiply your height in centimeters by 4.60
Warning: These multipliers will give you shorter RADs than you typically find on fashionable bikes. Bikes have gotten longer but people haven’t.”
At the time, I read the articles and understood exactly what he was talking about. It’s an obvious concept for those of us that design and fit bicycles. Rather than using the handlebar end stack and handlebar end reach, McCormack combines the coordinates making one number. Good enough. He neglects to apply an angular value to the dimension (later, RAAD) but, as we all know, the bike pitches enough during riding that the angle is less crucial than the distance but does describe the natural stance of the fit and how it will perform generally when climbing, traversing, or descending.
The problem that stands out with this method is that McCormack makes the mistake applying the wrong factor to the wrong measure. 4.47 is preposterous as a usable number just as using the rider’s height to arrive at this. I could say, “Multiply your pinky length by 13”, and that would be about as silly as the way that McCormack is arriving at his number. It may work well for novice rider that is lost in left field but it doesn’t work for a real all-around bike or a truly fast bike. It’s not a useful or professional system. We all have different arm lengths compared to our bodies and we are all positioned on a bike that reflects what works for our given terrain and goals.
I think the big problem is that McCormack is an older guy and he doesn’t get to ride on bikes with modern geometries (He’s a Specialized shill). He’s basically stuck with retail Specialized product to ride. He also works with a ton of novice riders that are looking for easy confidence. That’s not my world. I get to ride anything I dream up, test it, re-build it, and go fast on. A totally different understanding and need.
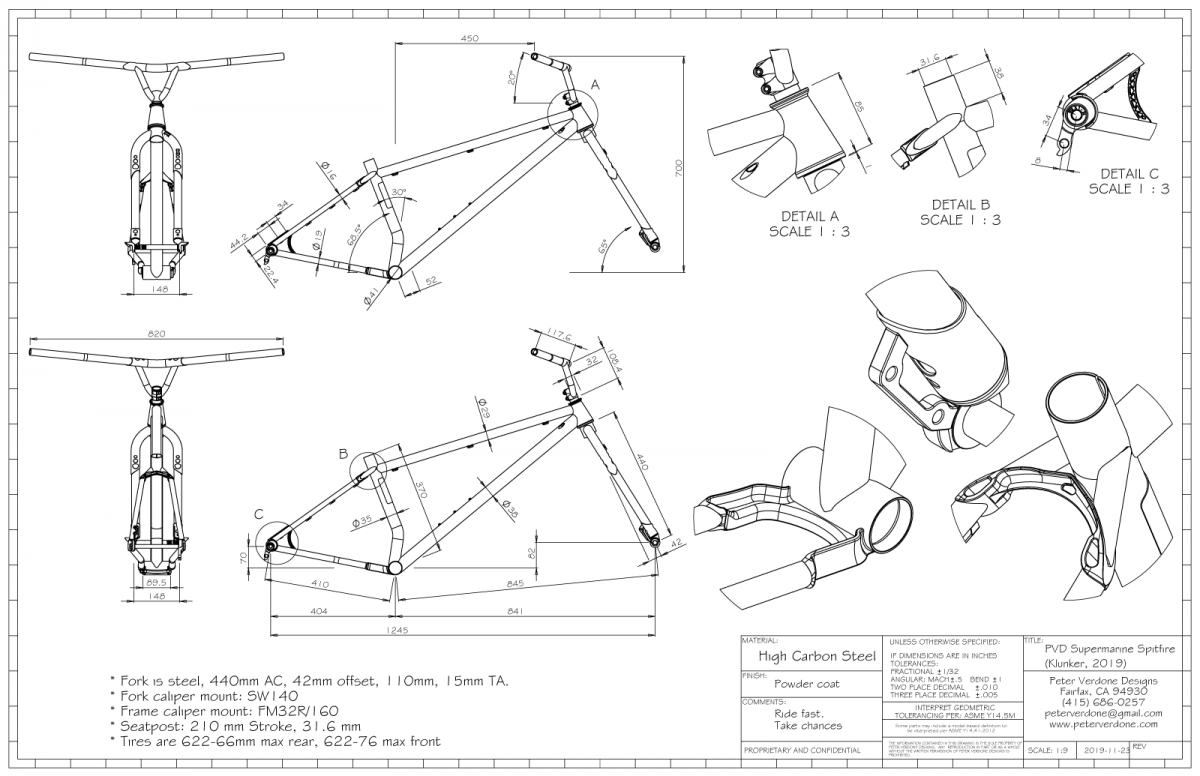
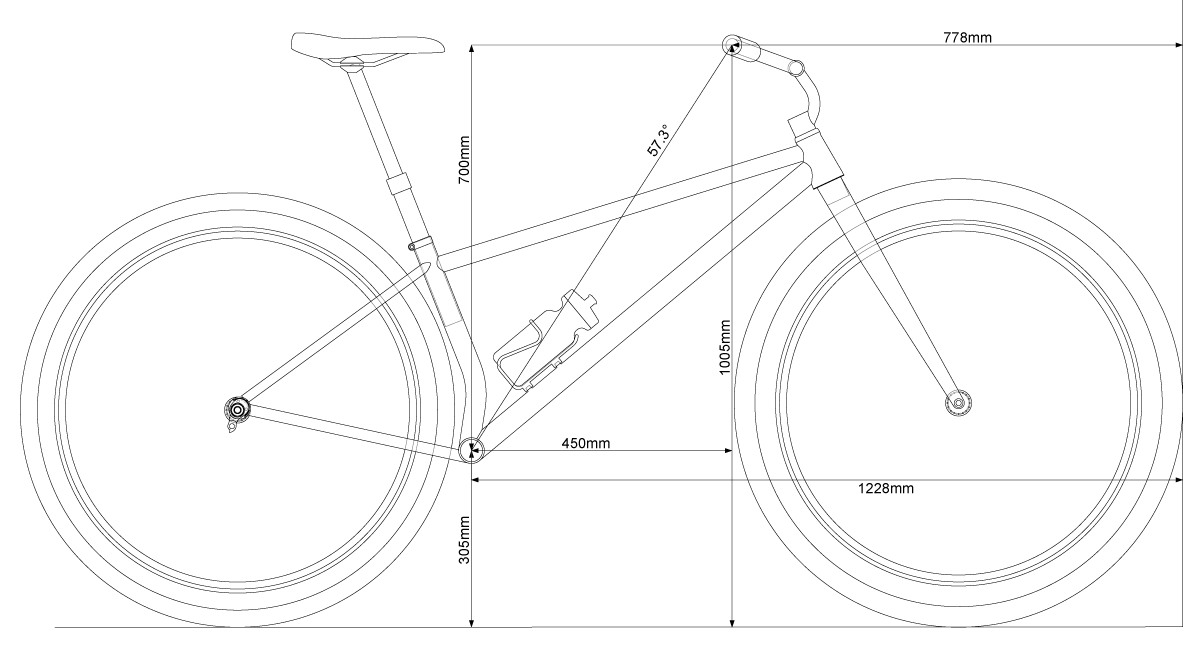
I forgot about McCormack’s LLB-RAD stuff for the last year. I didn’t need it with its bad factor. I was busy with other projects and rabbit holes.Then, earlier today, I was preparing a nice print of a bike that I’ll be finishing when I get back from a road trip with my wife. Here it is:
I was staring at the print. I do this a lot as it helps generate fresh ideas. I’m trying to find ways of showing what I wanted to show when I thought of the LLB-RAD number. I decided to look at it with regard to this bike. Remember, this new bike is a klunker, with nearly the same fit as my Sopwith Camel but an improved geometry. It’s not my fastest bike. It’s for casually having fun on: chilling out on a lake loop or bombing down the trail with the boys.
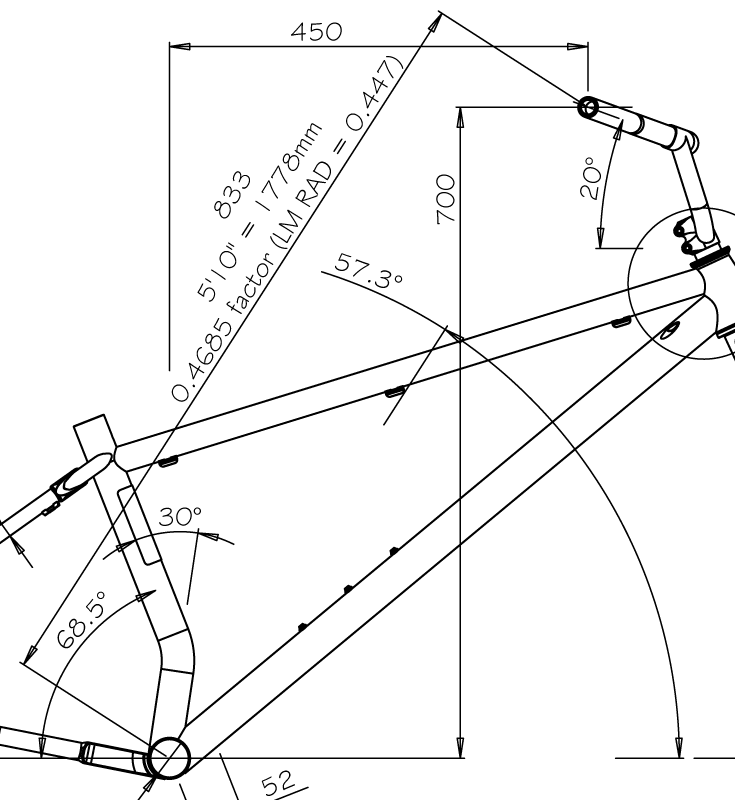
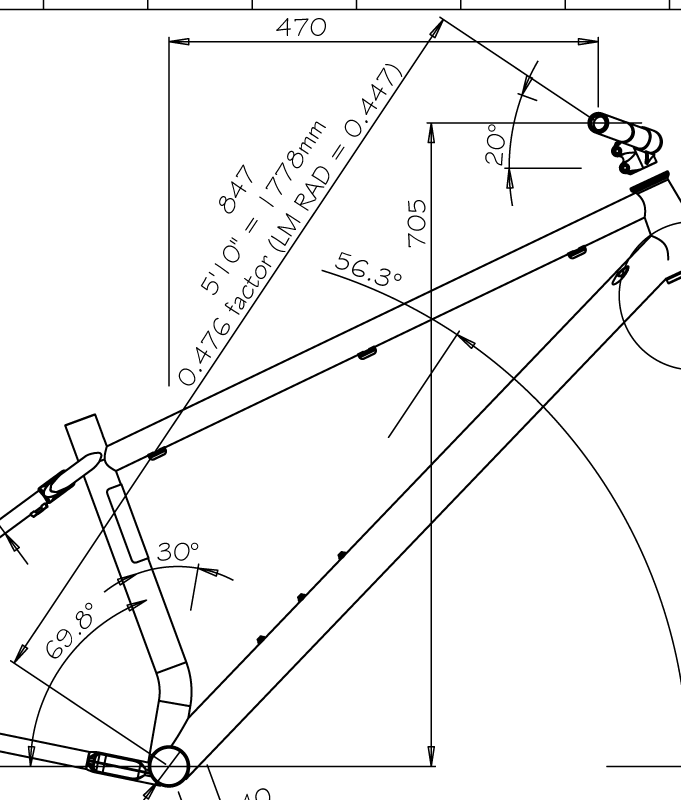
At 5’10”, I get a LLB-RAD factor of 0.469 at a 57.3 degree angle, not the 0.447 that McCormack recommends. If I had used that, I’d be sitting at 795mm instead of 833mm. That’s a 38mm difference. In the world of bike fit, this is a gigantic difference. Imagine if your saddle was 38mm too high or low.
I’m no uber-XC roadie climber bro. I’m an overweight, 49 year-old shredder that climbs to the top of the Marin hills and bombs as fast as I can down the hardest trails that I can find. I no longer race and wasn’t a star when I did. I can take a rest whenever I like but I demand that I beat others to the bottom of the trail…or at least do my level-headed best to make that happen. Basically, I’m an average guy. So it’s telling how erroneous McCormacks numbers are in my case.
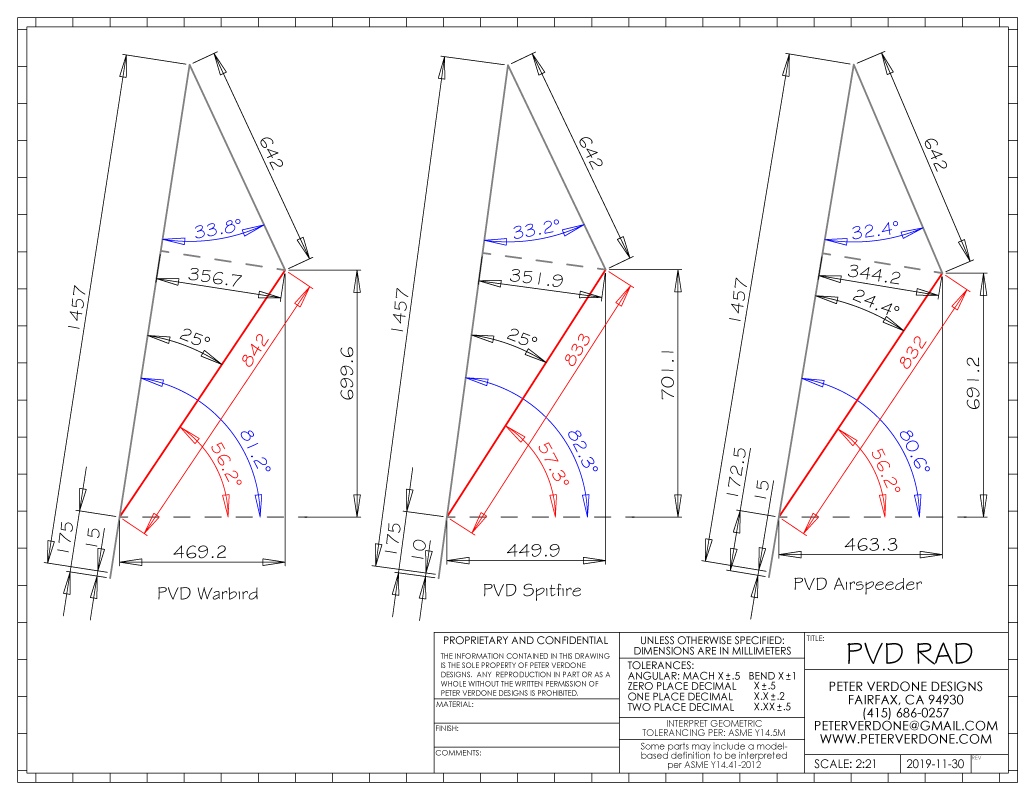
So, to be fair, McCormack isn’t talking about fully rigid goofball klunkers with 16 degree back sweeps. He’s talking about trail/enduro bikes. OK. Let’s look at my Warbird. A 180mm forked hardtail that goes insanely fast and often outruns fast guys on FS bikes. This is a more fair comparison.
A note, the geometry for the Warbird is shown with the fork sagged 30% and a 9 degree backsweep to the bars. The sweep of the bars is a factor as it changes the actual arm length interaction with the grip, although we are measuring to the end of the grip for convenience.
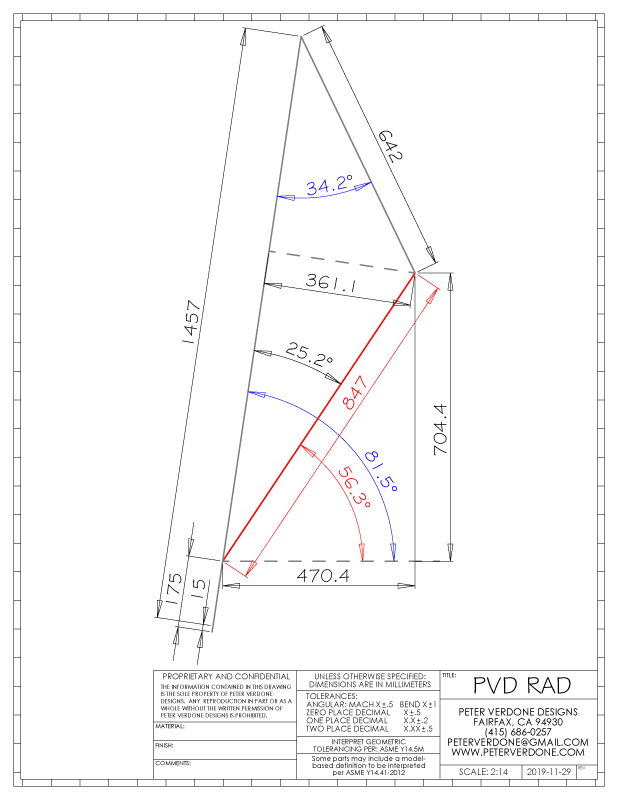
It only gets worse for LLB-RAD methodology on this bike. Here, I have a 0.476 factor at a 56.3 degree angle. 847mm instead of 795mm. A 52mm difference. A degree lower than the klunker but also 1.7% longer. This is explained by the difference in the goal of the bikes and the margin of error that is provided with a big suspension fork on the front of the Warbird. On the other hand, the Warbird is 6.5% longer than what LLB-RAD would recommend. Significant.
These aren’t flukes. They are precise fit numbers on highly tested and developed platforms for an area that represents a wide variety of riding schemes. I ride both bikes on double black diamond trails in the area, I’m not slow, and I’ve got more than 30 years of riding experience on mountain bikes. I’ve also been focusing on mapping all of this kind of stuff for the last 16 years.
Another obvious problem with the LLB-RAD factoring is that it doesn’t consider the differences in arm length to body size. Someone who falls outside of ‘normal’, like having a large or small ape index will never work well. It also doesn’t help us translate the fit and scheme of one rider to another or one rider among their different bikes. Something better has to exist.
Examining the bottom bracket to handlebar end measurement is one of the most important things we can do in mountain bike fit and design. I use this for designing my bikes but most often in the X/Y coordinate view, although I have preferred ride testing positions. A translation system would be a huge boon for me. I could more accurately place another rider on the bike with a clear understanding of the changes being made for performance and their different body dimensions.
Let’s forget about connecting a factor to height. That makes no sense. Instead, let’s look at the right angle formed by the arm socket to grip and the arm socket to sole. For me roughly, I have an arm length, socket to grip, of 642mm and a height from the ground of 1457mm. Directly, that’s 1592mm. Comparing that to the 847mm bar to bottom bracket dimension from my Warbird, we get a factor of 0.532. For the Spitfire, 0.523. While this is a lot more accurate than what Lee proposes, it isn’t great or super informative.
Instead, let’s get more specific to actual measures and meanings. Maybe a rubric or algorithm exists if we get into the weeds.
We have the two measures from our body, and add two more from our bike, pedal and shoe. The bike measures don’t really change from one paradigm to another unless you are changing pedals and shoes (as I do in these two examples). The other two, body angle from ground and arm angle from body define the fit. The body angle is changed per the rider preference and might remain constant from one bike to another or change slightly if the bikes use changes. The arm angle from the body will depend on the front center of the bike and the uphill demands by the terrain and rider.
It is important to have the hands at the appropriate spacing when taking this measure. If you don’t have a set of handlebars with grips in place, use a broomstick with a bit of masking tape marking the ends for bar spacing. For most average men, this will be about 780mm. Women will probably be around 760mm. You’re mileage may vary. This is a whole different discussion.
Some folks are talking about using the front of the acromion, a process of the scapula for measuring the arm pivot. I need to look into this more as the more accurately we can place the pivot the better but this isn’t a pure hinge and the point of pivot travels some. The shoulder is an extremely complex joint as explained in the video below.
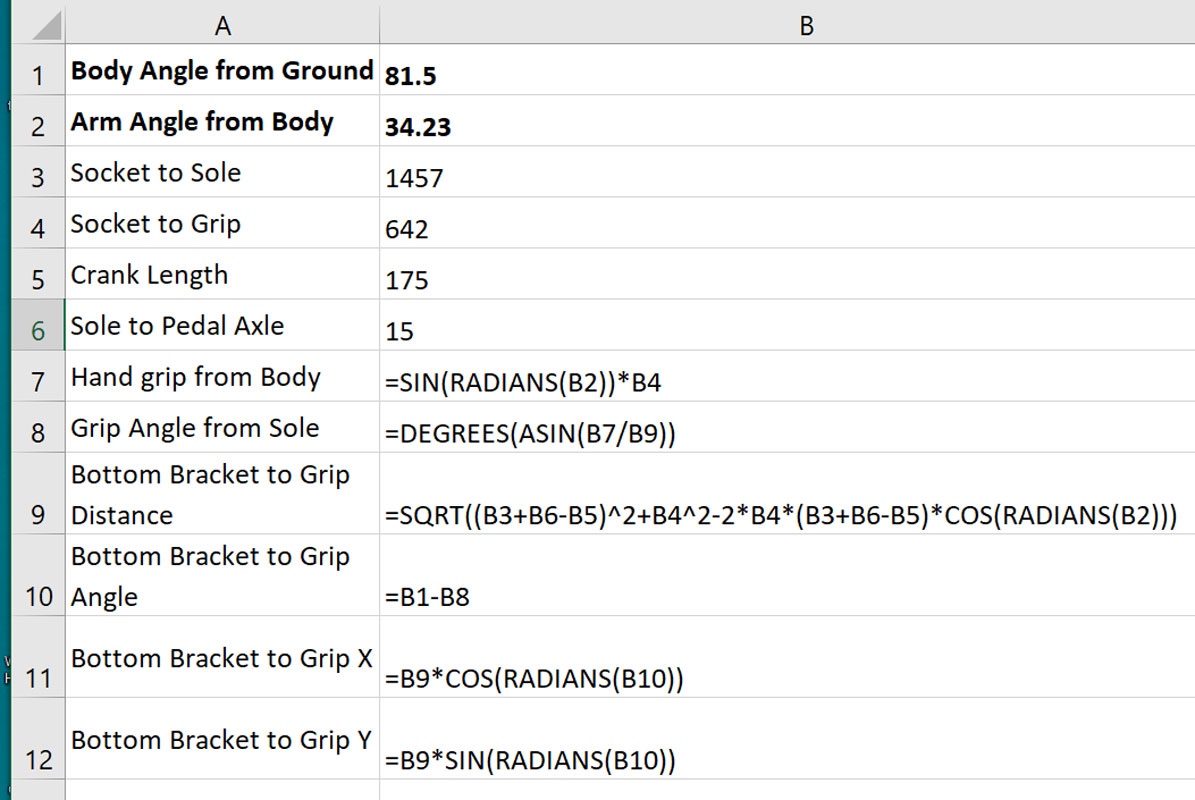
Let:
Body Angle from Ground (B1) = 81.50 degrees
Arm Angle from Body (B2) = 34.23 degrees
Sole to Arm Socket (B3) = 1457mm
Arm Socket to Grip (B4) = 642mm
Crank Length (B5) = 175mm
Pedal Axle to Sole (B6) = 15mm
Body to Hand Grip (B7) = SIN(B2) * B4= SIN(34.23) * 642 = 361.1 mm
Grip Angle from Sole (B8) = ASIN(B7/B9)) = ASIN(361.1/847.0) = 25.2 degrees
Bottom Bracket to Bar End (B9) = SQRT((B3+B6-B5)^2+B4^2-2*B4*(B3+B6-B5)*COS(B2)) = SQRT((1457+15-175)^2+(642)^2-2*(642)*(1457+15-175)*COS(34.23)) = 847.0mm
BB to Bar End Angle from Ground (B10) = B1 + B8 = 25.2 + 56.3 = 56.3 degrees
In case you were wondering, the math here I used the Law of Cosines to calculate B9. Trigonometry is super important in life!
If you have a proper drawing of your bicycle fit and geometry, you will be able to use the existing position of your bike to adjust the angles to close in on the correct values. If nothing else, this process should make obvious the value and importance of keeping up to date prints within reach.
Remember, this isn’t really about where the handlebars are. This is about where your body is positioned over the bike and how you move over it. If we know how we want our body to end up (in general) we can place the bars in a way that works with our arm length and chassis.
Stand on one of the pedals (bottom of stroke) with leg extended while riding. Extend arms straight to handlebars keeping body in line. Have a friend note the angle of the arms from the body and body angle to the ground. This would be a reference stance. This is just a comparative reverence as almost any other position to fit the bars are impossible to duplicate without significant measure and modeling.
Looking at a few of these numbers for the Spitfire, we see an arm angle from the body of 33.24 degrees and a body angle from the BB of 82.30 degrees, just a bit more relaxed than the Warbird
Once a baseline of useful angles are gathered, it becomes far easier to fit a rider to a bike or model a custom frame beneath them.
This is untested but it is relating to actual measures of fit rather than an arbitrary factor off the top of one’s head. The “Arm Angle from Body”, here 34.23 degrees is the value in question. The preferred value will be one that works for you in the geometry paradigm that you are using. If you are on an old fashioned bike, it may be shallower. If you are on a modern bike and are an aggressive climber it may be broader.
Below, I compare 3 very different bikes; The 180mm forked hardtail Warbird, the full rigid klunker Spitfire, and the flat bar all-road Airspeeder. It’s interesting how close they are and what is changing just slightly on each.
It does appear that with with more data from riders of other sizes, this can work.
You may ask, “Why make this so complicated?” I’m not. This function is a simplification of what is really happening, that accounts for a few of the variables in question. How a rider relates to a bicycle is very complicated and dynamic. We try to simply our rules of thumb but if we go too far, we aren’t doing anything. I’m trying to produce utility here.
Of course, like any ‘rule of thumb’ this is not an accurate model. That would be impossible without trackside point tracking and rendering in 3D space. So what do we do? We look for something that works to help predict our needs as different rider bodies on different terrain with different strengths and skills….on different bike designs. That’s a lot to pack in. Too complex and we get lost in the weeds. Too general (LLB-RAD) and it’s completely useless.
You can easily measure your own bike for the location of the bar end by placing it against the wall, taking a few measured from the wall and floor to your handlebar end and bottom bracket, then do a little arithmetic. I show this simply below.
I feel that this system does give a useful resultant based on the 4 inputs. The problem at this point is finding out how to generalize the two angular fields. More, the simple measure of just the arm socket location is proving to be difficult to produce accurately and repeatedly among folk. That is where my work on this is going now. I may have to visit some kinesiologists for some help.
This as a tool would be a boon for me as a designer, especially given my current te techniques. Necessity is the mother of invention and I need this tool.
I’m going to stew on this more. This needs further investigation. While I’m not a fan of ‘off the bike’ fitting, getting to a real usable system of translation would be good. I’ll give Brent @BikeCAD a call and see if he’ll get this measure added to his program.
I tell people to measure their bikes all the time. They never do. Really. NEVER. Measure your bike! Test this crap out before you believe it. You can start understanding bicycle geometry instead of just talking about it.
Be careful what you read and what you believe. You get what you put in.
Also, unlike McCormack, I don’t allow my bike to get ruined by having handlebars in the correct position. I solved that problem long ago, ala the #beancan.
