Skateboard steering is a very challenging thing to model. I’m used to doing some incredibly complex calculations for my bicycle projects but producing this calculator pushed me to my limit. It took me three days of full time work to finally get the math correct.
I had done a calculator like this 20 years ago. I didn’t want to trust that old work as I’ve gotten a bit better at modeling and math since. So I ignored the earlier work and started this fresh. I wanted it dead right.
Somehow, I came up with the steering geometry math pretty quickly, about 6-7 hours. Honestly, I can’t even remember how I did it but it worked. That’s how lost in the weeds I got. If you’re thinking that 6-7 hours of work to get a few equations is crazy, you haven’t done anything complex yet.
It was the wheelbase decay that was the hardest to figure. I needed this to precisely calculate the steering radii. I missed one important assumption early on and it almost had me give up entirely. I hadn’t got to the point of crying but I was just a few hours away from that. This is a great example of how persistence and ‘stick-to-it-ness’ really win the day over raw intelligence. I’m not the smartest guy in the world but I don’t give up when the project is important enough. Here it was.
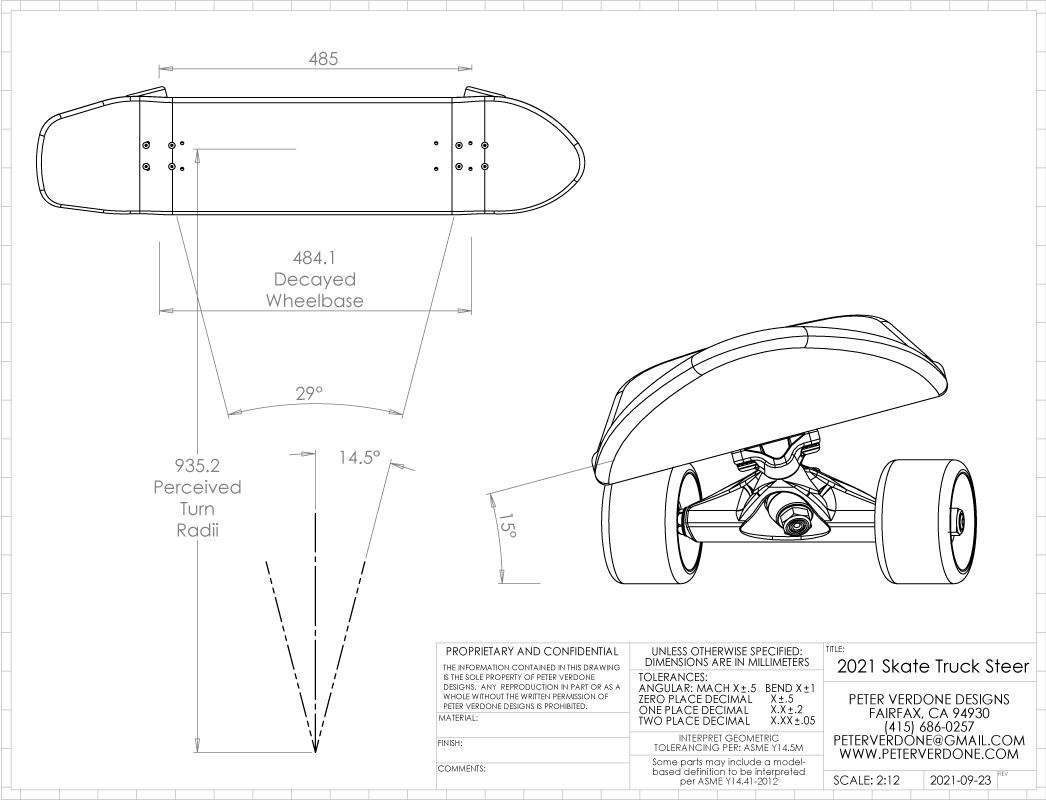
Below we can see a drawing of the skateboard that I’m currently working on. It’s got a nice comfortable 485mm wheelbase. Most larger size standard skateboards are in the 435mm range. This is 50mm longer. This makes cruising on rough streets and standing on the deck significantly more comfortable. I love this setup.
When talking about skate steering, the perceived turning radii for a given amount of deck tilt will tell most of the story. Depending on the conditions of use and rider preference, we can set a rough target before production and testing begins.
For 15 degrees of deck tilt, we see a, ‘sub-meter’, 935.2mm radii. This is very good for tight navigation on crowded city sidewalks and subway platforms.
Working in the modeling environment is crucial for developing parts for production and nice graphics but it doesn’t give us a lot of power for quick visualizations of the behavior that matters. For this, we move to spreadsheets. (this is where the math gets hard).
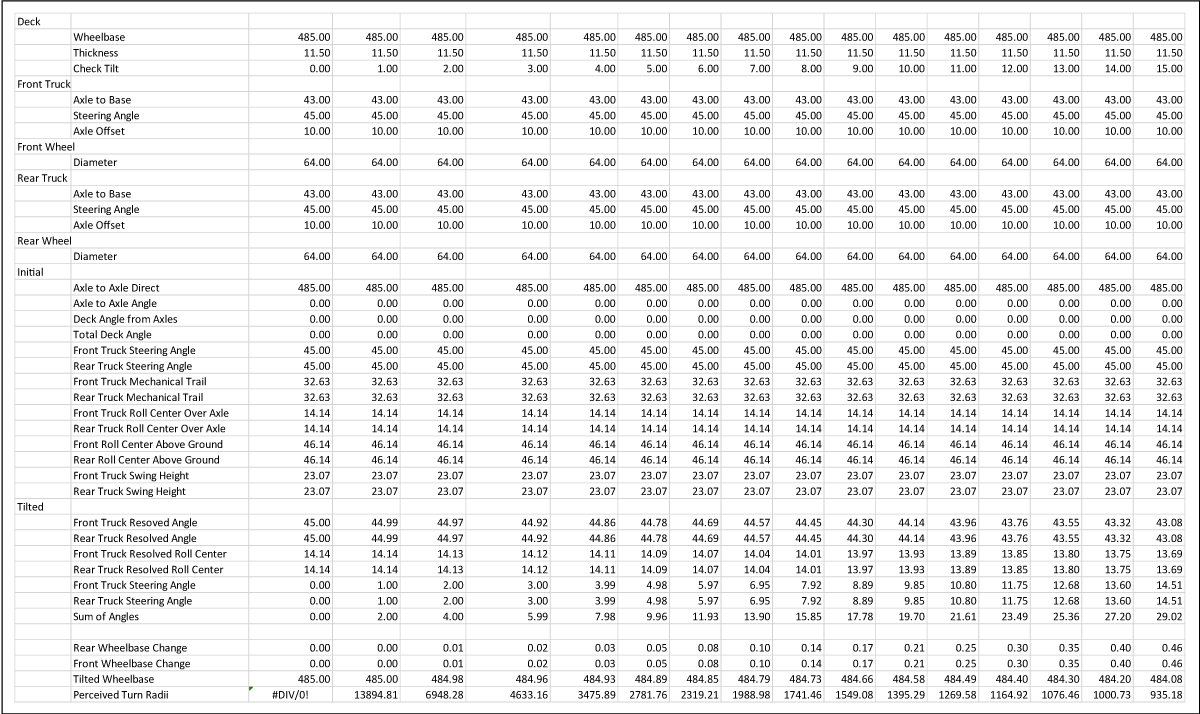
Below is a calculator for this deck. It’s not been cleaned up yet or made pretty but it’s accurate and precise. We can get real values given many different configurations and states in one quick view.
These values were all confirmed against solid models to 8 decimal places for matching front and rear setups. The math is spot on. The numbers are good. When the front and rear truck geometries are different, there are some complex changes that are not accounted for but these are very small and not worth the time to eliminate given that these types of setups are extremely rare outside of slalom racing.
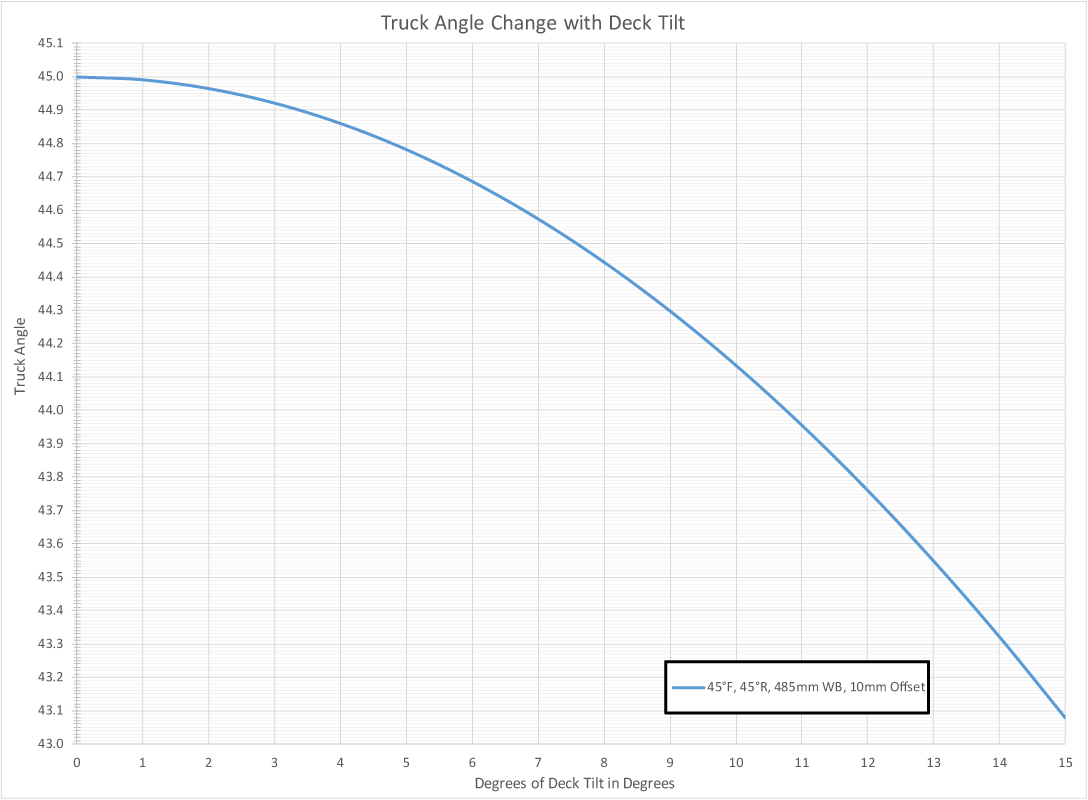
Then we plot these values against other possible setups. Here, we can see that while this skateboard has a 50mm longer wheelbase, it’s quicker handling that a short board with customary ‘quick’ turn commodity trucks. If we had a response that we knew was perfect for our needs, we could target that for any geometry.
We also see that most of the work of the system has been done in the first 7 degrees of deck tilt, and we only get another meter from the last 8 degrees of tilt.
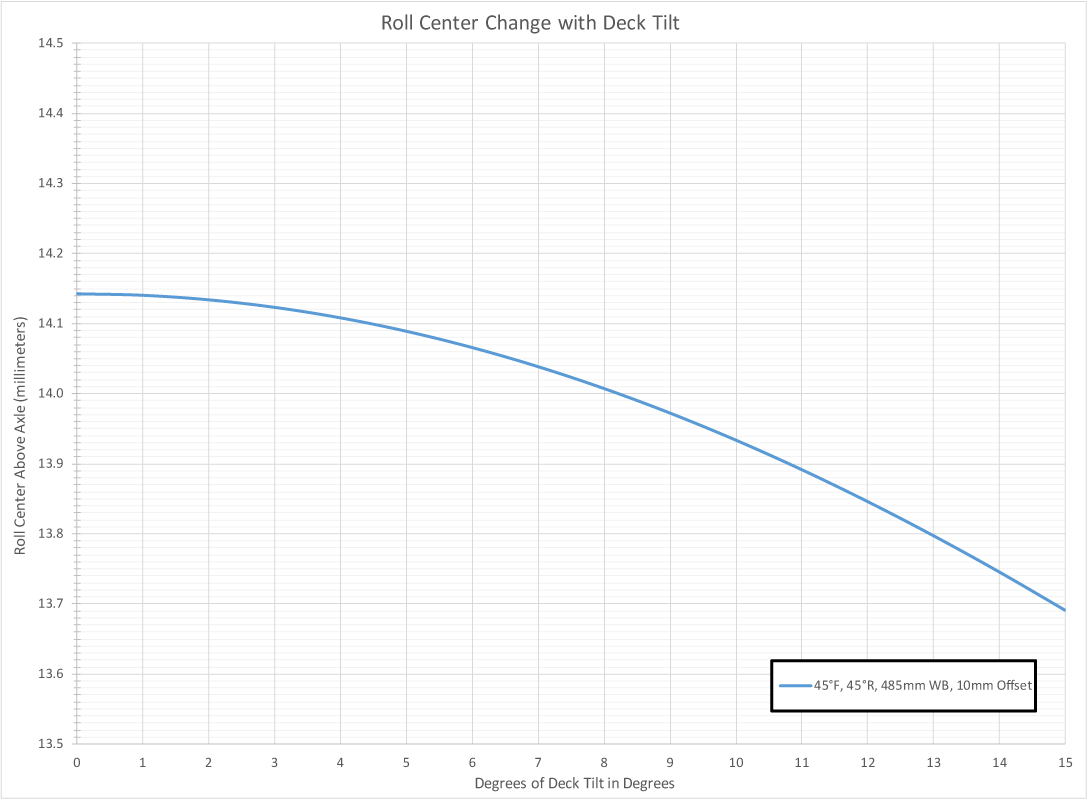
Also, we see that the offset that that the axles take from the steering axis have no effect on the steering geometry of the skateboard. That value is important when it comes to the forces going through the system though so it should not be ignored.
The complexity in all of this is that the pivot axis lays on an inclined plane. When the deck is tilted that plane is tilted and the resulting axis angle is a combination of the two.
Having this data tells us many things. Here we can see how the roll center drops as the deck is tilted. It’s something that isn’t even visible when manipulating the solid models but it is happening in a very very small way, 0.45mm.
I can never stress enough how important trigonometry is. None of the calculations here relied on any advanced mathematical operation beyond simple algebra and trigonometry. What was the challenge was seeing the path to the solution and keeping track of a good deal of geometries.